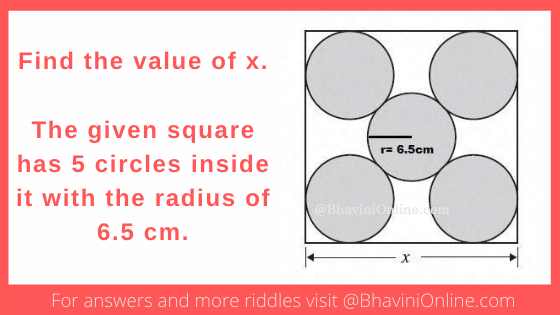
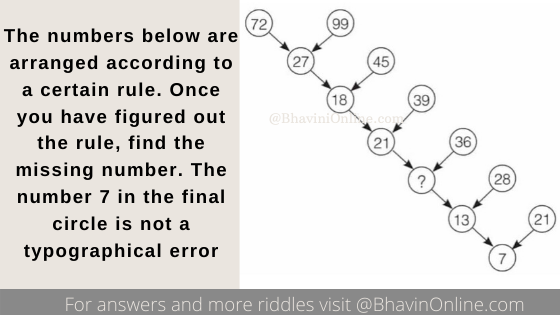
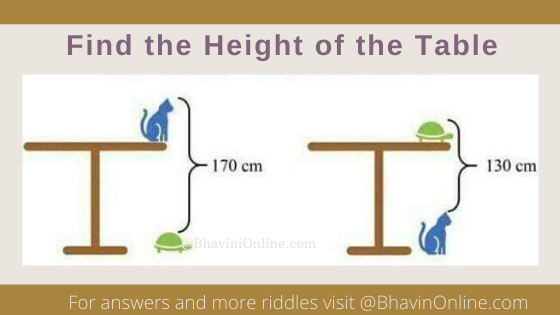
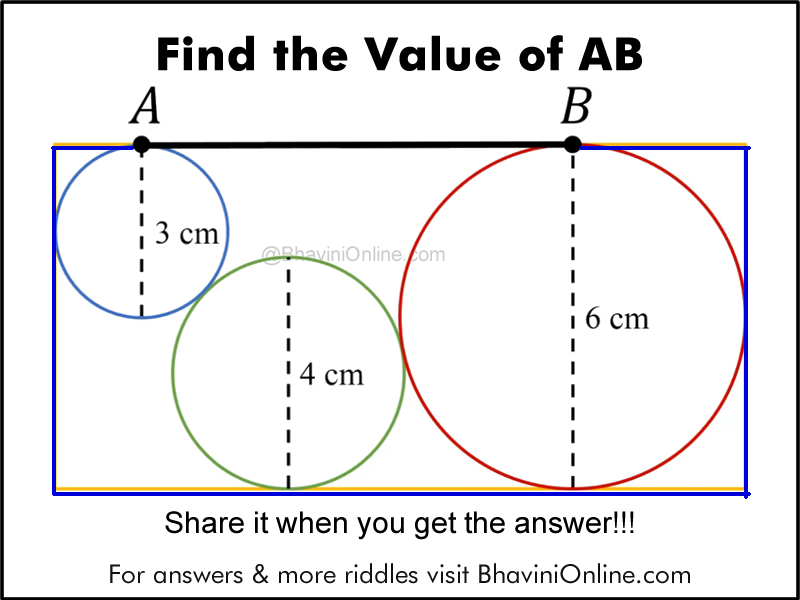
Math Riddle: What Is the Side of the Square Which Has 5 Circles With 6.5 Cm Radius?
Test your geometry skills with this picture riddle. In the given picture you will see a square which has 5 circles inside it. The radius of the circle is given as 6.5 cm. Can you find the value of x? So were you able to solve the riddle? Leave your answers in the comment section … Read more